Ryan Munseong Jeong

I am a developer with 2 years of experience. My main programming language is C, but I also know at good level C++ and Golang. You can read more about me in the About section.

2 minute read

소프트웨어

컴퓨터(universal turing machine)라는 “마음의 도구”를 다루는 방법

  • 소프트웨어(turing machine): 지혜와 언어로 짜고 짓는
  • 소프트웨어는 무섭다: 구체적인 실천 (단지 스위치들의 집합, 주어진 명령을 묵묵히 수행하는)
    • 소프트웨어는 사람이 만들고 기계가 실행함

소프트웨어를 잘 만들 방법

알고리즘(algorithm) 언어(language)
일하는 방도 표현하는 방식
푸는 솜씨 담는 그릇
박차 고삐

개괄

소프트웨어는 튜링기계다. 튜링기계는 어떤 일을 하고, 그 일은 어떤 문제를 푸는 것이다. 컴퓨터는 그 소프트웨어(튜링기계)를 실행하면서 문제풀이를 자동으로 진행하는데, 이때 “컴퓨터로 문제를 푼다”는 것이 이 뜻이다. 컴퓨터로 돌릴 소프트웨어를 만드는 것이다.

  • 푸는 솜씨, 알고리즘과 복잡도
    • 소프트웨어(튜링기계)로 만드는 문제 푸는 방도
    • 컴퓨터 문제 풀이법
    • 비용의 계층
    • 컴퓨터로 풀 수 있는 쉬운 문제와 어려운 문제의 경계
  • 담는 그릇, 언어와 논리
    • 소프트웨어(튜링기계)를 표현하는 언어
      • 튜링기계의 규칙표 방식은 매우 원시적
      • 사람에게 좀 더 편한 방식 요구
        • 쉽게 작성되고, 쉽게 검증할 수 있어야
    • 언어의 계층. 번역과 실행
    • 프로그래밍 언어의 두개의 중력
    • 프로그래밍 = 논리증명

알고리즘

알고리즘은 컴퓨터로 돌릴 수 있는 문제푸는 방도

  • 하나의 소프트웨어 = 하나의 튜링기계
  • 소프트웨어(튜링기계)는 어떤 문제를 푸는 것
  • 컴퓨터는 소프트웨어를 실행 = 문제풀이를 자동으로 진행

묻게된다:

  • \( \exists \) 더 좋은(싸고 빠른) 방법?
  • 있다면 얼마나 더 좋은가?
  • 더 좋기는 불가능한가?
  • 경계는 어디인가?
    • 현실적인 비용으로 해결가능한 문제들
    • 그렇지 않은 문제들

알고리즘 예

  • 책읽기
  • 자연수 \( n(n \geq 2) \)이 주어졌을 때 \( 1 \times 2 \times \cdots \times n \) 을 계산하기
  • 주머니의 숫자중에서 제일 큰 숫자를 찾기
  • 장보기 목록에 있는 모든걸 장바구니에 담았는지 확인하기
  • 그녀가 마음속에 품은 자연수 알아맞추기. 1부터 n사이에 있다. 그녀는 예/아니오만 답할 수 있다.
  • \( a^{n} = \underbrace{a \times \cdots \times a}_\text{n} \) 계산하기
  • 뒤죽박죽인 숫자를 크기순서로 나열하기
  • 패스워드 해킹하기
  • 자연수 인수분해하기

알고리즘 복잡도

  • 시간과 메모리 소모량
  • 입력크기의 함수로
  • 결국 어떻게 되는지(asymptotic complexity)

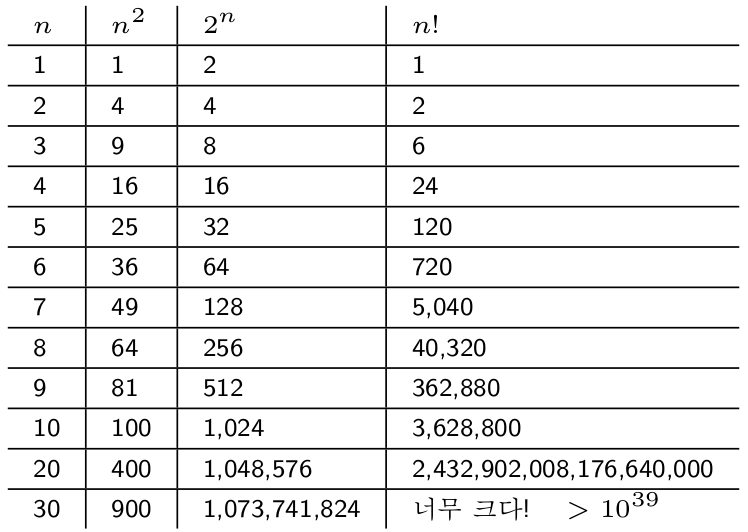
ch03-algo-complex

복잡도 증가 속도

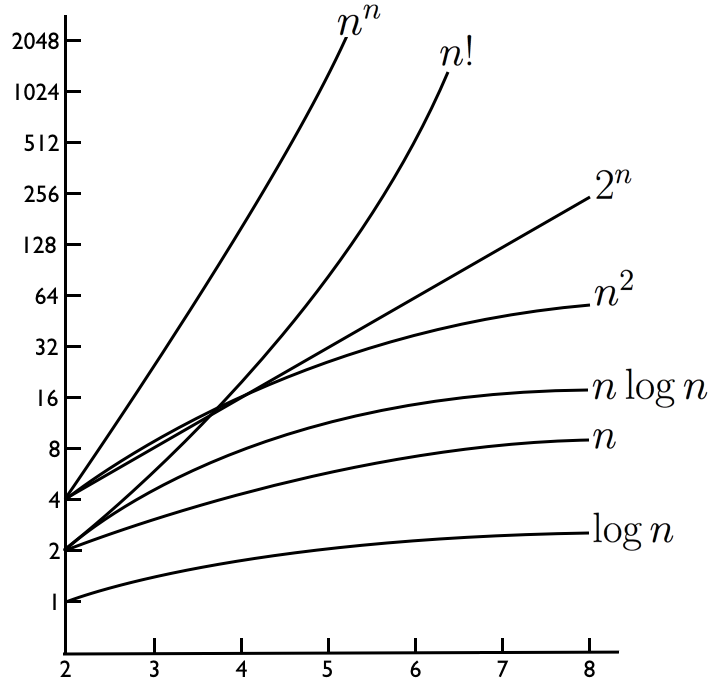
ch03-000

알고리즘 복잡도 표기법

\( O(f(n))\)

  • (입력크기 \( n \) ) = \( f(n) \)의 상수배보다 작다는 뜻
복잡도 알고리즘 스텝 횟수가
\( O(1) \) 상수이면
\( O(\log{n}) \) \( \log{n} + 10\), \(9871 \log{n} + 100 \) 등이면
\( O(n) \) \( n + 10\), \(999n + 9\), \(2016n - 18 \) 등이면
\( O(n^{2}) \) \( 999n^{2} + 9\), \(2016n^{2} + 199000n - 18 \) 등이면
복잡도 \( n \)이 두 배가 되면 일컫기를
\( O(1) \) 변함없다 상수 constant
\( O(\log{n}) \) 약간의 상수만큼 커진다 로그 logarithmic
\( O(n) \) 두 배 커진다 선형 linear
\( O(n \log{n}) \) 두 배보다 약간 더 커진다 엔로그엔 n log n
\( O(n^{2}) \) 네 배 커진다 제곱배 quadratic
\( O(n^{k}) \) (상수 \( k \) ) \( 2^{k} \)배 커진다 k승배, 다항 polynomial
\( O(k^{n}) \) (상수 \( k \gt 1 \) ) \( k^{2} \)배 커진다 기하급수배 exponential
\( O(n!) \) \(2^{2} \)배 정도 커진다 계승배 factorial

알고리즘 복잡도 예

  • 책읽기
    • \( O(n) \)
  • 자연수 \( n(n \geq 2) \)이 주어졌을 때 \( 1 \times 2 \times \cdots \times n \) 을 계산하기
    • \( O(n) \)
  • 주머니의 숫자중에서 제일 큰 숫자를 찾기
    • \( O(n) \)
  • 장보기 목록에 있는 모든걸 장바구니에 담았는지 확인하기
    • \( O(n^{2}) \)
  • 그녀가 마음속에 품은 자연수 알아맞추기. 1부터 n사이에 있다. 그녀는 예/아니오만 답할 수 있다.
    • \( O(n) \) (worst), \( O( \log_{2}{n}) \) (best)
  • \( a^{n} = \underbrace{a \times \cdots \times a}_\text{n} \) 계산하기
    • \( O(n) \) (worst), \( O( \log_{2}{n}) \) (best)
  • 뒤죽박죽인 숫자를 크기순서로 나열하기
    • \( O(n^{2}) \) (worst), \( O( n \log_{2}{n}) \) (best)
  • 패스워드 해킹하기
    • \( O(10^{n}) \)
  • 자연수 인수분해하기
    • \( O(10^{n}) \)

Leave a comment

You may also enjoy