SNU 046.016 컴퓨터과학이 여는 세계(Computational Civilization) Part I

컴퓨터라는 도구

• 인류역사에 유례가 없던 도구
• 컴퓨터의 놀라운 점은 뭘까?
  • 컴퓨터 vs. 칼, 활, 바퀴, 고무밴드, 자동차, 냉장고, ···
  • 컴퓨터 = “만능”
• 도구 사용법
  • 컴퓨터 = “마음의 도구”

  컴퓨터	다른 도구
  글쓰기	힘쓰기
  마음, 지혜	팔다리 근육

• 컴퓨터, 마음의 도구, 만능 기계

컴퓨터 원천 설계도 “탄생비화”

“보편만능의 도구(universal machine)”

• 20세기 수학의 좌절을 재확인하는 데 동원된 소품
• 이것이 20-21세기 정보혁명의 주인공이 되는 아이러니

수학자들의 꿈

수리명제 자동판결 문제(_{Entscheidungsproblem, decision problem})
1928년 @ 국제 수학자대회(ICM)

David Hilbert(-1943)

모든 명제들의 첨/거짓을 “기계적”으로 판명할 수 없을까?

참인 모든 명제들을 “기계적”으로 만들어낼 수 없을까?

(자연수에 대한 단순_first-order 사실들을)

“기계적”

• 생각없이 할 수 있는
• 단순작업으로 되는
• 자동으로 동작하는

1931년, 수학계의 “좌절” 혹은 “희소식”

Kurt Gödel(-1978)

“기계적인 방식만으론 사실인지 판정할 수 없는, 그런 명제가 존재한다.”

• 튜링소년이 자신만의 방식으로 다시 한 번 증명
  • 튜링의 증명속 소품으로 등장 = 컴퓨터의 원천설계도

“계산가능한 수에 대해서, 수리명제 자동판별 문제에 응용하면서”
“On Computable Numbers, with an Application to the Entscheitungsproblem” Proceedings of the London Mathematical Society, ser.2, vol.42 (1936-37). pp.230-265; corrections, Ibid, vol 43(1937) pp.544-546

• 1934년 11월, Cambridge U 학부졸업논문 제출
• 1935년 봄, Part III course on Foundations of Mathematics 수강(강사: Max Newman)
• Newman의 강의는 Gödel의 불완전성의 증명(Incompleteness Theorem)으로 마무리됨
  • “QQ기계적인 방식WW으로는 참/거짓을 판명할 수 없는 명제가 존재한다.”
  • Newman: “참/거짓을 판명해주는 QQ기계적인 방식WW은 있을 수 있겠지 …”
• Newman 강의를 수강 후 1935년 초여름,
  • 1935년 4월 말, group theory에 대한 논문 제출 및 출반(London Mathematical Society). 이 논문은 폰 노이만 논문을 작게 개선한 것.
  • 1935년 양자역학 연구를 할까 생각하며 수리물리학 Fowler 교수를 찾아가 연구꺼리를 얻었으나 진전이 없었음
  • Newman이 강의 때 던진 말이 튜링의 관심을 붙듦
• 이때 즈음, 장거리 달리기 취미를 가진 튜링 왈, “달리기를 마치고 풀밭에 누워 있는데 힐버트의 세 번째 문제를 어떻게 풀지가 생각나더라.”

튜링의 1936년 논문

[설득] 기계적으로는 모든 참인 명제를 만들 수 없다.

1. 과감히 정의: “기계적”을 정의
2. 그리고 보임: 기계적인 작업의 한계

튜링의 정의: “기계적”이란 …

“기계적” = 튜링기계(TM)로 돌아가는 정해진 네 가지 부품(테잎 박스, 기계 상태, 심볼 박스, 규칙표 박스)만으로 만든 기계로 돌리는 …

• 무한: 빈칸이 무한히 많은 테잎
• 유한: 기계상태들 \( \Bbb R \subseteq \Bbb S \times \Bbb T \times \Bbb T \times \{ \gt, \lt, \Arrowvert \} \times \Bbb S \)

튜링기계의 한 예:

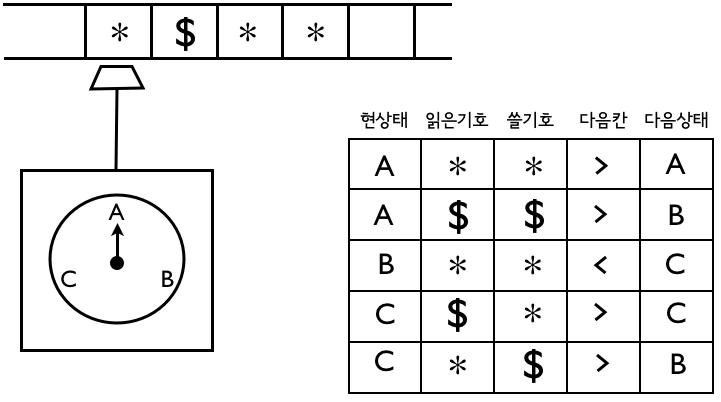
튜링기계 하나 = 기계작업 하나

더하기 튜링기계, 카톡 튜링기계, 유튜브 튜링기계, 등등

소품으로 등장한 특이한 튜링기계 하나

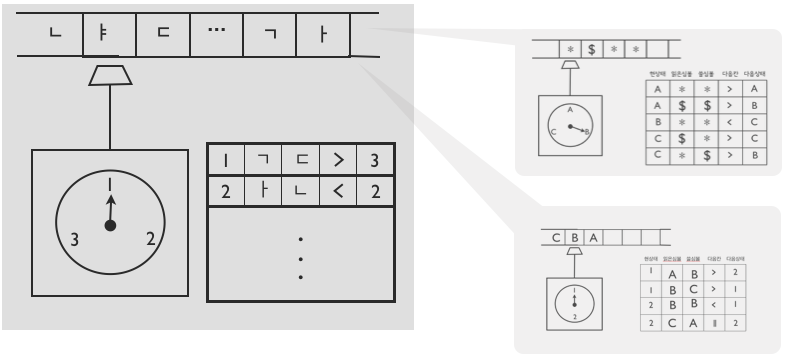
만능 튜링기계_{universal machine}
하나의 튜링기계, 그러나 “만능”

• 입력: 튜링기계를 글로 표현해서 테잎에 받는다
• 출력: 그 튜링기계의 작동을 그대로 따라한다

컴퓨터 = 만능 튜링기계_{universal machine}

• 사용법: 임의의 튜링기계(소프트웨어) 테잎에 싣기
• 자동작동: 테잎에 있는 튜링기계 그대로 따라하기(실행)

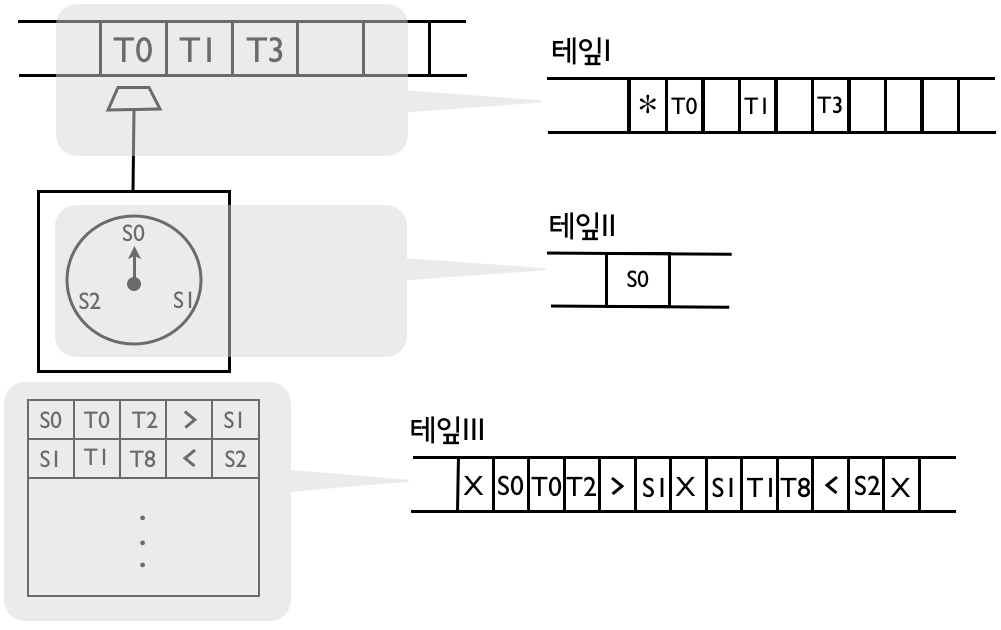
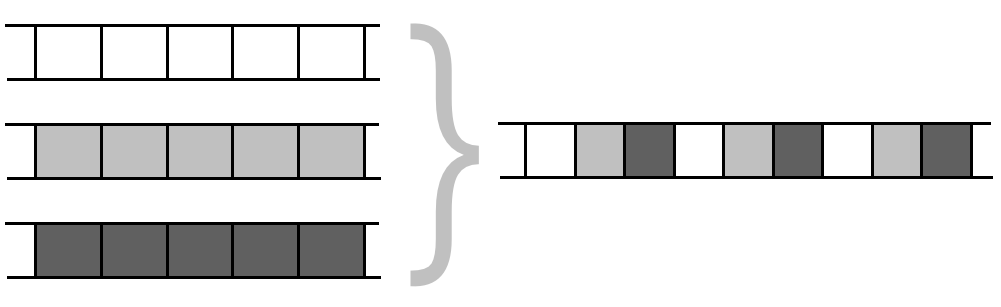
• 아래 과정을 반복함
  1. 읽기: 테잎II에서 현재상태 심볼 S_i
  2. 읽기: 테잎I에서 위치심볼(*)의 테잎심볼 T_j
  3. 규칙찾기: S_i와 T_j가 매치되는 규칙을 테잎 III에서 찾기
  4. 찾은 규칙이 시키는 일 하기: 심볼 복사 + 위치 심볼 이동

튜링의 1936 논문

[설득] 기계적으로는 모든 참인 명제를 만들 수 없다.

1. 과감히 정의: “기계적”을 정의
2. 그리고 보임: 기계적인 작업의 한계

튜링 증명의 지렛대: 만능기계 & “셀 수 있음”

• 어떤 튜링기계건 정해진 유한개 부호의 글로 표현가능

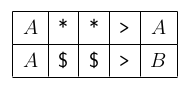
• 상태 심볼 {A, B, C}는 {S₀, S₁, S₂}
• 테이프 심볼 {*, $}는 {T₀, T₁}
• 따라서 일렬로 표현하면
  • A  *  *  > A   끝 A  $  $  > B
  • S0 T0 T0 > S0  X  S0 T1 T1 > S1
• 즉, S, T, 0, …, 9, <, >, ||, X로 표현한 16진수
  • marker 더하면 17진수
    • 테잎 한 칸이 두 개의 저장 공간을 갖고 있다고 생각해 보라
    • 한 쪽엔 위치 정보를 기록하는 marker(*)를 기록하고, 다른 한 쪽엔 정보를 저장
• 세 개의 테잎을 각각 자연수 N₁, N₂, N₃으로 나타내면, 소인수분해 개념을 이용해 하나의 자연수로 만들 수 있음
  • 2^N₁ X 3^N₂ X 5^N₃

튜링의 증명

• 사실1: VERI 가능하면 H 가능 (\(\color{teal}{\exists VERI \Rightarrow \exists H}\))
  • 참인 명제를 모두 술술 만드는 튜링기계(VERI)가 존재한다면, 그 기계로 멈춤문제를 풀 수 있다(H).
• 사실2: H 불가능 (\(\color{teal}{\nexists H}\))
  • 멈춤문제를 푸는 튜링기계는 존재할 수 없다.

따라서, 기계적으로는 모든 참인 명제를 만들 수 없다.

증명 준비

• 튜링기계의 개수는 무한히 많지만, 자연수의 개수를 넘을 수 없다.
  • 튜링기계마다 자연수 하나(17진수의 자연수)에 대응
• 무한의 세계에도 크기 차이가 있다.
  • 칸트로(Georg Cantor)의 대각선 논법
    (\( | \Bbb N | \lt | 2^{\Bbb N} | \))

사실 1: \(\exists VERI \Rightarrow \exists H\)

만일 모든 참인 명제를 만드는 튜링기계(VERI)가 존재한다면, 그 기계로 멈춤문제를 푸는 기계(H)를 만들 수 있다. 왜?

기계 H를 다음과 같이 만들 수 있다.

1. 기계를 입력받는다 (M 이라고 하자)
2. 만능기계로 VERI 를 실행시킨다
3. VERI는 모든 참인 명제를 만들므로, 언젠가는 “M은 멈춘다” 또는 “M은 멈추지 않는다”를 만들 것이다
4. 만드는 데로 답하면 된다

이므로.

사실 2: \(\nexists H\)

자연수로 모든 튜링기계와 입력을 번호매길 수 있다: M₁, M₂, ···, I₁, I₂, ···.

1. 만약 H를 만들 수 있으면, 다음 테이블을 모두 메꿀 수 있다.

\[\begin{array}{r|lll} \ & I_1 & I_2 & ··· \\ \hline M_1 & 1 & 1 & ··· \\ M_2 & 1 & 0 & ··· \\ ··· & ··· & ··· & \end{array}\]

1. 그러면 모든 튜링기계와 다른 튜링기계 X를 만들 수 있다! X = 입력 I_n 마다 M_n 과 다르게 작동하도록(대각선논법)
     = Table(M_n , I_n) = 1 이면 M_n 돌린결과+1 아니면 1

X(n) = UM(M_n, I_n) X H(M_n, I_n) + 1

1. M₁, M₂, ··· 가 다가 아니고 X 가 또 있다고? 말이 안 되네. 그러네, H 는 있어서는 안 되네.

튜링의 증명: 사실1 + 사실2. 끝

• 사실1: VERI 가능하면 H 가능 (\(\color{teal}{\exists VERI \Rightarrow \exists H}\))
  • 참인 명제를 모두 술술 만드는 튜링기계(VERI)가 존재한다면, 그 기계로 멈춤문제를 풀 수 있다(H).
  • VERI: 힐베르트 교수가 찾고자 했던 기계 (참인 명제들을 하나도 빠뜨리지 않고 만들어내는 기계)
  • H(Halting problem): 글로 표현된 튜링기계를 돌렸을 때, 영원히 돌 것인가, 어느 순간에 멈출 것인가를 정확히 답할 수 있는 기계
• 사실2: H 불가능 (\(\color{teal}{\nexists H}\))
  • 멈춤문제를 푸는 튜링기계는 존재할 수 없다.

따라서, 기계적으로는 모든 참인 명제를 만들 수 없다.

기억: 튜링 증명(1935년 논문)의 5개 아이디어들

1. 튜링기계
2. 튜링기계를 글로 표현하기
3. 글로 입력된 튜링기계를 돌리는 만능 튜링기계(컴퓨터)
4. 글로 입력된 튜링기계가 끝날지 미리 판단하는 문제
5. 대각선논법: “그것 말고 더 있어요” 설득기술

---

• References:
  • 이광근. (2015). 컴퓨터과학이 여는 세계. 인사이트.
  • 이광근. (2016). SNUON_컴퓨터과학이 여는 세계 [video file]. Retrieved May 27, 2018, from https://www.youtube.com/watch?v=HTWSPoDLmHI&list=PL0Nf1KJu6Ui7yoc9RQ2TiiYL9Z0MKoggH.
  • 이광근. (2016). SNU 046.016 컴퓨터과학이 여는 세계(Computational Civilization) Part I [PowerPoint slides]. Retrieved May 27, 2018, from http://ropas.snu.ac.kr/~kwang/046.016/15/1h4in1.pdf.