컴퓨터과학의 원천 아이디어가 나오기까지(카오스재단 강연)

컴퓨터라는 도구

• 인류역사에 유례가 없던 도구
• 컴퓨터의 놀라운 점은 뭘까?
  • 컴퓨터 vs. 칼, 활, 바퀴, 고무밴드, 자동차, 냉장고, ···
  • 컴퓨터 = “만능”

도구 사용법

• 컴퓨터 = “마음의 도구”

  컴퓨터	다른 도구
  글쓰기	힘쓰기
  마음, 지혜	팔다리 근육

컴퓨터, 마음의 도구, 만능 기계

컴퓨터 원천 설계도 “탄생비화”

“만능의 도구”

• 20세기 수학의 좌절을 재확인하는 데 동원된 소품
• 이것이 20-21세기 정보혁명의 주인공이 되는 아이러니

수학자들의 꿈

수리명제 자동판결 문제_{entscheidungsproblem}
1928년 @ 국제 수학자대회(ICM)

힐베르트(Hilbert)(-1943)

모든 사실을 “기계적”으로 만들 수 있을 것 같다?

(자연수에 대한 단순_first-order 사실들을)

“기계적”

• 생각없이 할 수 있는
• 단순작업으로 되는
• 자동으로 동작하는

1931년, 수학계의 “좌절” 혹은 “희소식”

괴델(Gödel)(-1978)

“기계적인 방식으론 모든 사실을 만들 수 없다.”

튜링소년이 자신만의 방식으로 다시 한 번 증명

• 튜링의 증명속 소품으로 등장 = 컴퓨터의 원천설계도

“계산가능한 수에 대해서, 수리명제 자동판별 문제에 응용하면서”
“On Computable Numbers, with an Application to the Entscheitungsproblem” Proceedings of the London Mathematical Society, ser.2, vol.42 (1936-37). pp.230-265; corrections, Ibid, vol 43(1937) pp.544-546

튜링의 1936년 논문

[설득] 기계적으로는 모든 참인 명제를 만들 수 없다.

1. 과감히 정의: “기계적”을 정의
2. 그리고 보임: 기계적인 작업의 한계

튜링의 정의: “기계적”이란 …

“기계적” = 튜링기계(TM)로 돌아가는 정해진 네 가지 부품(테잎 박스, 기계 상태, 심볼 박스, 규칙표 박스)만으로 만든 기계로 돌리는 …

튜링기계의 한 예:

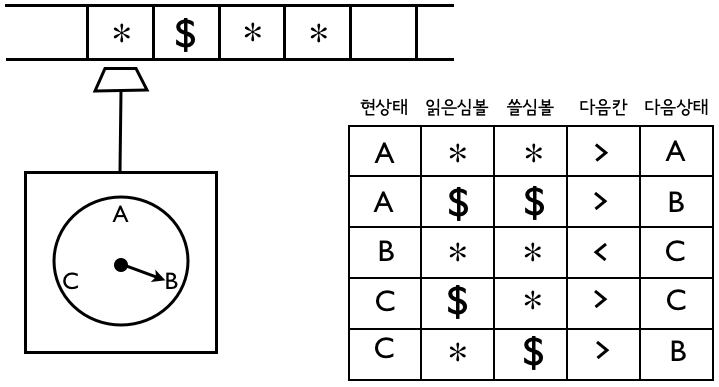
튜링기계 하나 = 기계작업 하나

더하기 튜링기계, 카톡 튜링기계, 유튜브 튜링기계, 등등

소품으로 등장한 특이한 튜링기계 하나

만능 튜링기계_{universal machine}
하나의 튜링기계, 그러나 “만능”

• 입력: 튜링기계를 글로 표현해서 테잎에 받는다
• 출력: 그 튜링기계의 작동을 그대로 따라한다

컴퓨터 = 만능 튜링기계_{universal machine}

• 사용법: 임의의 튜링기계(소프트웨어) 테잎에 싣기
• 자동작동: 테잎에 있는 튜링기계 그대로 따라하기(실행)

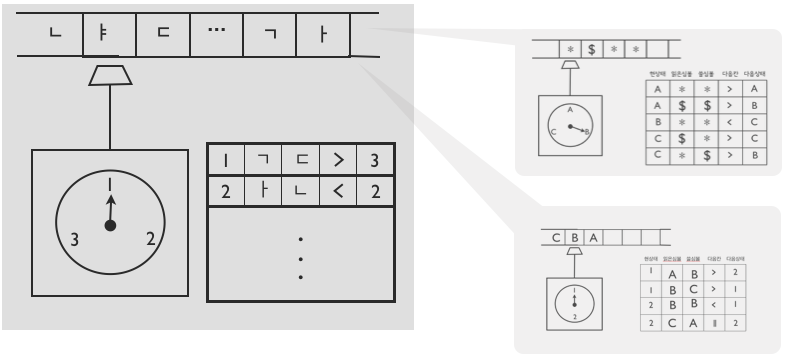
튜링의 1936 논문

[설득] 기계적으로는 모든 참인 명제를 만들 수 없다.

1. 과감히 정의: “기계적”을 정의
2. 그리고 보임: 기계적인 작업의 한계

튜링 증명의 지렛대: 만능기계 & “셀 수 있음”

• 어떤 튜링기계건 정해진 유한개 부호의 글로 표현가능

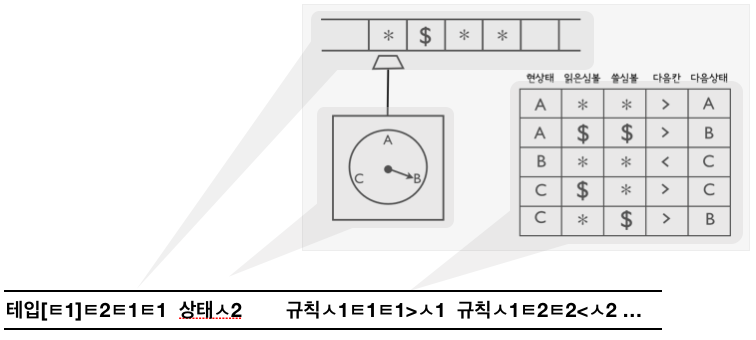
• 39개 부호 = 한글 24개 자모, 아라비아 숫자 10개, <, >, ||, [, ]
• 그런 글 = 39-진법의 자연수

튜링의 증명

• 사실1: VERI 가능하면 H 가능 (\(\color{teal}{\exists VERI \Rightarrow \exists H}\))
  • 참인 명제를 모두 술술 만드는 튜링기계(VERI)가 존재한다면, 그 기계로 멈춤문제를 풀 수 있다(H).
• 사실2: H 불가능 (\(\color{teal}{\nexists H}\))
  • 멈춤문제를 푸는 튜링기계는 존재할 수 없다.

따라서, 기계적으로는 모든 참인 명제를 만들 수 없다.

사실 1: \(\exists VERI \Rightarrow \exists H\)

만일 모든 참인 명제를 만드는 튜링기계(VERI)가 존재한다면, 그 기계로 멈춤문제를 푸는 기계(H)를 만들 수 있다. 왜?

기계 H를 다음과 같이 만들 수 있다.

1. 기계를 입력받는다 (M 이라고 하자)
2. 만능기계로 VERI 를 실행시킨다
3. VERI는 모든 참인 명제를 만들므로, 언젠가는 “M은 멈춘다” 또는 “M은 멈추지 않는다”를 만들 것이다
4. 만드는 데로 답하면 된다

이므로.

사실 2: \(\nexists H\)

자연수로 모든 튜링기계와 입력을 번호매길 수 있다: M₁, M₂, ···, I₁, I₂, ···.

1. 만약 H를 만들 수 있으면, 다음 테이블을 모두 메꿀 수 있다.

\[\begin{array}{r|lll} \ & I_1 & I_2 & ··· \\ \hline M_1 & 1 & 1 & ··· \\ M_2 & 1 & 0 & ··· \\ ··· & ··· & ··· & \end{array}\]

1. 그러면 모든 튜링기계와 다른 튜링기계 X를 만들 수 있다! X = 입력 I_n 마다 M_n 과 다르게 작동하도록(대각선논법)
     = Table(M_n , I_n) = 1 이면 M_n 돌린결과+1 아니면 1

2. M₁, M₂, ··· 가 다가 아니고 X 가 또 있다고? 말이 안 되네. 그러네, H 는 있어서는 안 되네.

튜링의 증명: 사실1 + 사실2. 끝

• 사실1: VERI 가능하면 H 가능 (\(\color{teal}{\exists VERI \Rightarrow \exists H}\))
  • 참인 명제를 모두 술술 만드는 튜링기계(VERI)가 존재한다면, 그 기계로 멈춤문제를 풀 수 있다(H).
  • VERI: 힐베르트 교수가 찾고자 했던 기계 (참인 명제들을 하나도 빠뜨리지 않고 만들어내는 기계)
  • H(Halting problem): 글로 표현된 튜링기계를 돌렸을 때, 영원히 돌 것인가, 어느 순간에 멈출 것인가를 정확히 답할 수 있는 기계
• 사실2: H 불가능 (\(\color{teal}{\nexists H}\))
  • 멈춤문제를 푸는 튜링기계는 존재할 수 없다.

따라서, 기계적으로는 모든 참인 명제를 만들 수 없다.

기억: 튜링 증명(1935년 논문)의 5개 아이디어들

1. 튜링기계
2. 튜링기계를 글로 표현하기
3. 글로 입력된 튜링기계를 돌리는 만능 튜링기계(컴퓨터)
4. 글로 입력된 튜링기계가 끝날지 미리 판단하는 문제
5. 대각선논법: “그것 말고 더 있어요” 설득기술

---

• References:
  • 이광근. (2018). 컴퓨터과학의 원천 아이디어가 나오기까지 [video file]. Retrieved November 13, 2019, from http://ikaos.org/ko/video/video01.html?kb_idx=1559&mode=view.
  • 이광근. (2019). 컴퓨터과학의 원천 아이디어가 나오기까지: 튜링의 1935년 이야기 [PowerPoint slides]. Retrieved November 13, 2019, from http://kwangkeunyi.snu.ac.kr/talk/kaos18.pdf.